fft与fftrl

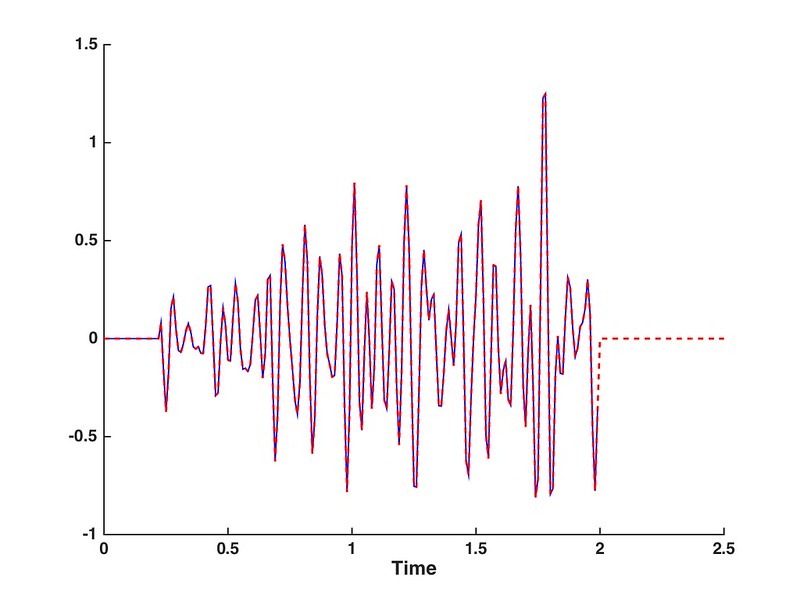
matlab内建的fft正变换结果，前一半是正频率，后一半是负频率；但是Margrave写的fftrl与ifftrl较为人性化的，仅考虑正频率部分。 [spec,f] = fftrl(s,t,p,n) 结果是包含第一个点直流分量+正频率半支的复数频谱； ifftrl(spec,f) 结果是将spec共轭部分补全，然后逆变换计算s。

如果之前正变换对时域有补零延长，那么该逆变换结果的就是补零延长之后的时域结果。 img

fft与互相关

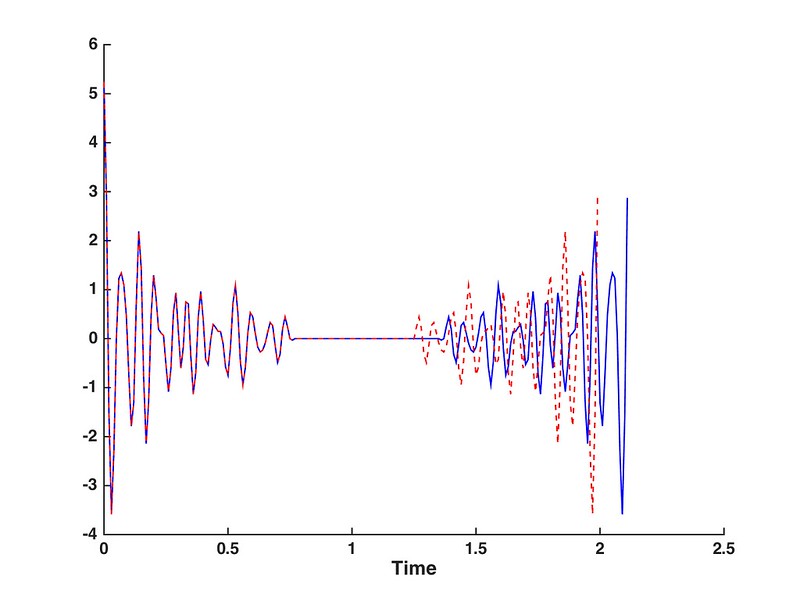
$COR(A,B) = B*conj(A)$ 在大数据的情况下，FFT计算互相关可以通过矢量化提高运算效率，相比xcorr节省更多时间。其逆变换结果前一半是互相关的正支，后一半是互相关的负支，因此必须要ifftshift才能与真实顺序一致。

对于奇偶点数，ifftshift之后的互相关正负半支的起始点位置不同，给定FFT点数为N，则正半支对应 $floor(N/2+1):N$;负半支对应 $floor(N/2+1)-mod(N,2)👎2$。

对于没有ifftshift的互相关结果 img

逆变换的正确姿势

一般情况下，我们会在频域对信号进行处理，比如滤波等，处理之后再逆变换回时域。

  1. 正逆变换的点数必须一致
  2. IFFT的输入的交流分量必须是共轭对称的 通常为了减少计算量，我们在频域只选择正半轴信号进行处理，那么处理之后的频域信号，严格来说需要添加一个共轭对称的另一半才能进行逆变换。 幸运的是MATLAB的ifft函数可以自动补偿共轭部分。

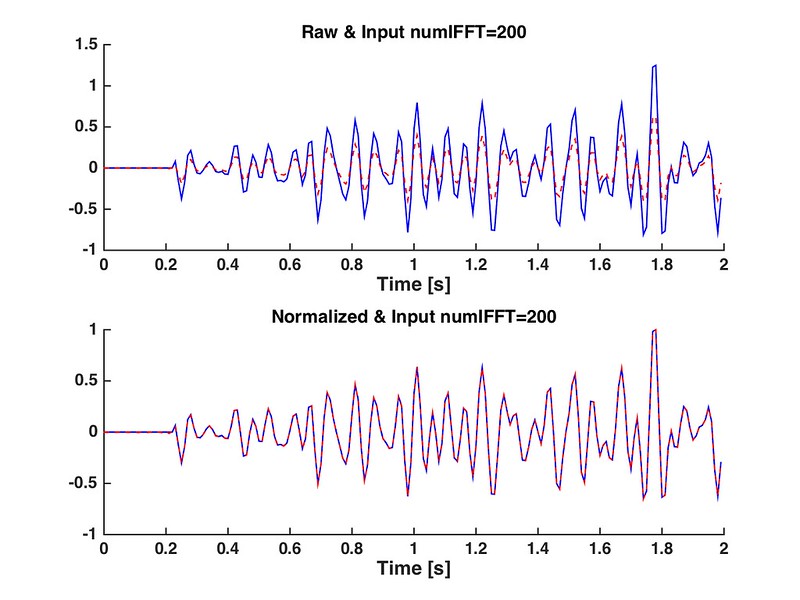
假定原始信号为A(1:N)，N=200，FFT变换结果为IA = FFT(A,512)

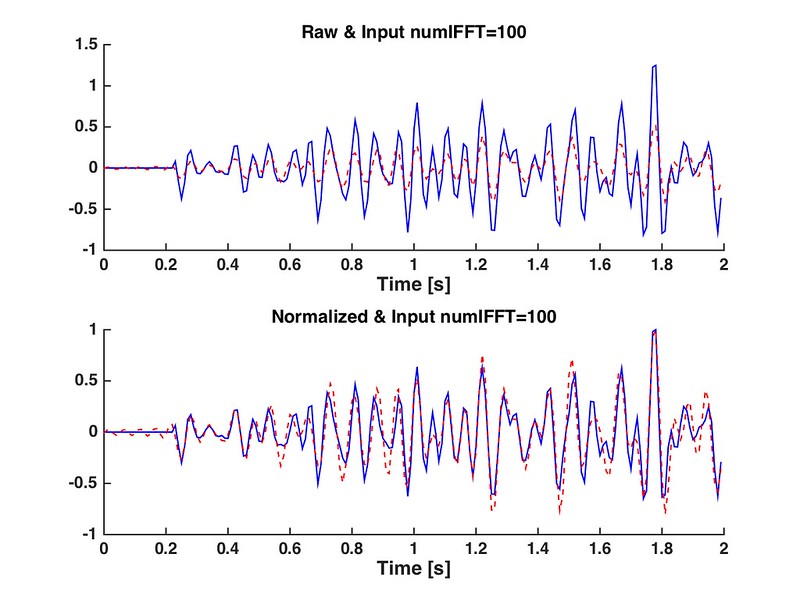
  1. 如果逆变换输入点数=N，时域结果就是多了个比例因子，相位不发生变化 img200

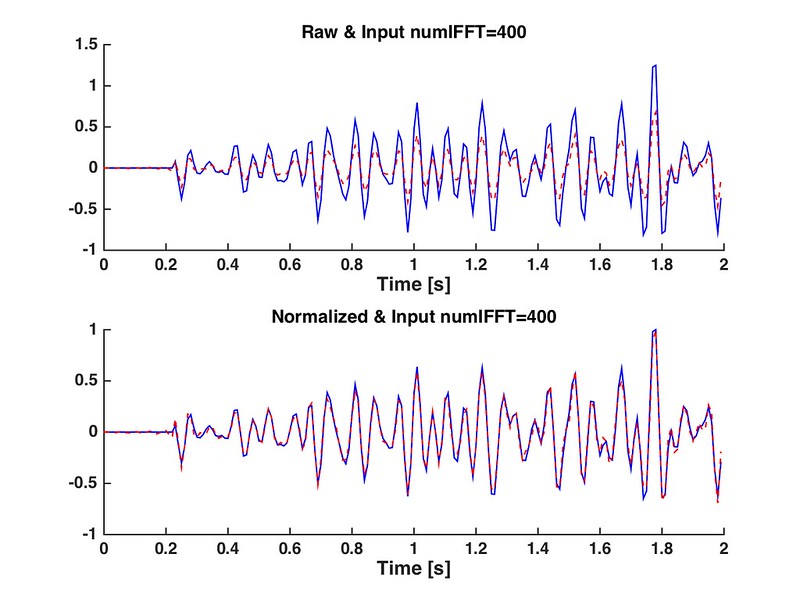
  2. 如果逆变换输入是大于N或者小于N，时域结果相位会发生一定程度的变化 img400 img100